Hung-yi Lee AI Lesson

Hung-yi Lee的AI课（2021version）笔记

Introduction of ML

机器学习的几种常见类别：
- Regression：输出为标量（scalar），如预测明日的PM2.5含量
- Classification：给定一些备选类别，让机器从中选择符合的，如垃圾邮件的判断；下棋从这个定义上而言，实际上也是一种classification，相当于当前每个能下的位置为分类当中的一个类别
过去人们，普遍认为就上面两大类，但时至今日，人们发现实际上还有诸如structured learning（创造结构化的输出，如图片、文档等）等类别，这也代表人们对ML的越来越高的期望。
常用的一些术语：model, feature, weight, bias, loss, label
MAE(mean average error) & MSE(mean square error)是loss function中的一些常用loss计算方式。对于概率预测，还有交叉熵(cross entrophy)可以作为loss function
梯度下降法（gradient descent）对于model中的多个参数，现选取一个起始点，再逐个参数进行梯度下降。对于梯度下降的步伐大小，一部分取决于该点的偏微分斜率大小，一部分取决于自定义的一个常数$\eta$，而这个常数就是模型的超参数了
总结来看，训练包括三个步骤：
1. 建立有未知数的方程
2. 根据训练数据设定loss function
3. （使用梯度下降法）优化
由于model自身不能很好描述情况的限制被称为model的bias
任意的函数都可以表示/近似表示成一个常数加一系列激活函数的集合，如：

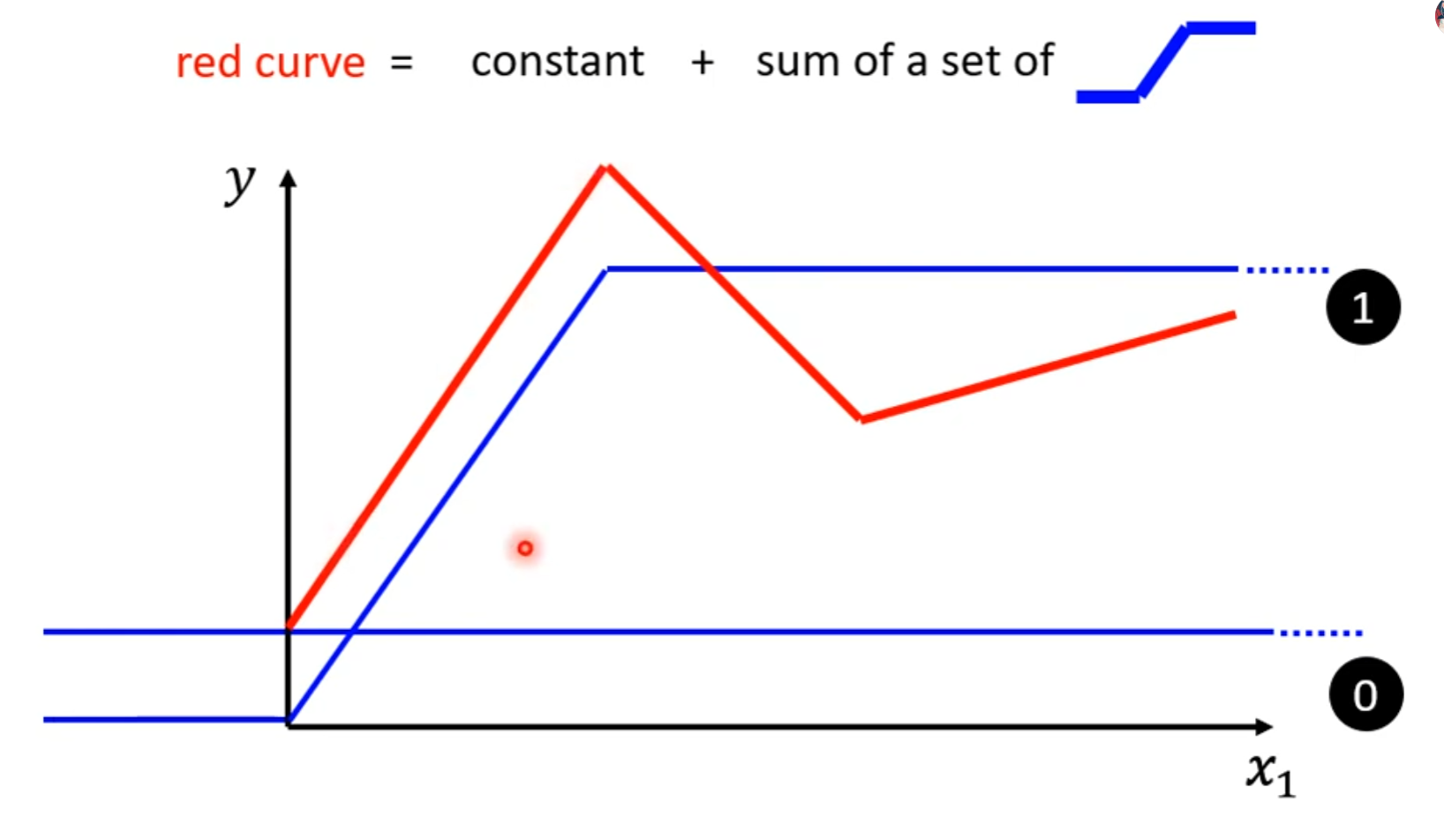
这种一个常数加一系列激活函数的集合的函数曲线形式称为piecewise linear curves
首先介绍的激活函数便是sigmoid函数，使用该函数来近似表示piecewise linear curves为 $y = b + \sum_ic_isigmoid(b_i+w_ix_i)$

如果考虑多个特征的输入（也就是y取决于一系列$x_1, x_2, … x_j$的输入），则该式变换为： $y = b + \sum_ic_isigmoid(b_i+\sum_jw_{ij}x_j)$

也就是有如下的形式（取j=3，即3个输入特征时）

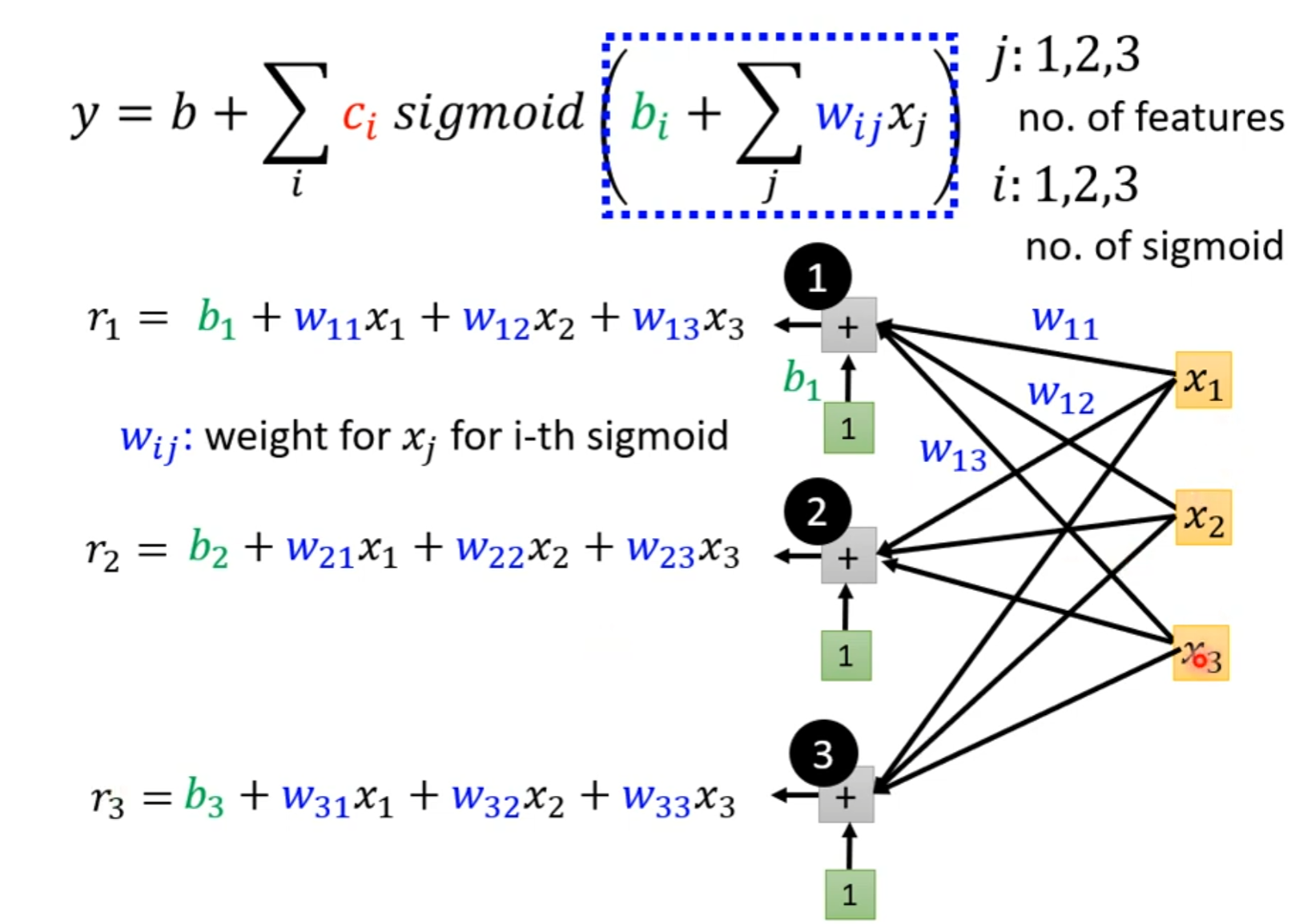
这样就有了MLP中的输入层形式。总体的形式如下：

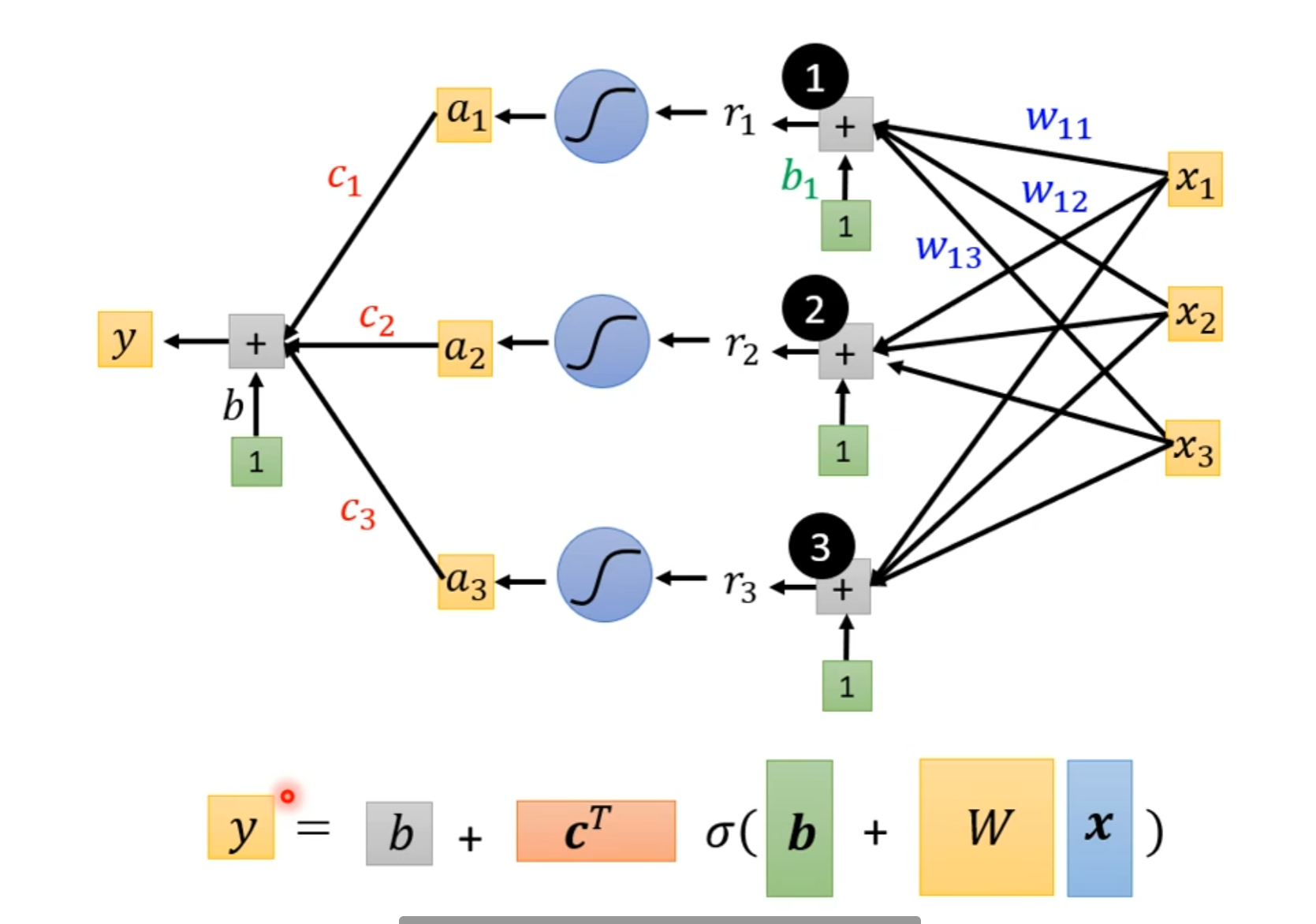
需要注意的是，上面的图只是一个示例，实际上网络的结构不光取决于输入的特征数量，其中的激活函数的数量也是可以作为超参数来自由定义的（而不只是像图中这样和输入的特征数量一致）这实际上就形成了一个网络结构。其中的$\boldsymbol{x}$为特征feature，$W, \boldsymbol{b}, \boldsymbol{c}^T, b$为未知参数unknown parameters，将未知参数中的每一个具体的参数值拼成一个长的向量，这个向量使用$\theta$来表示。相应的，loss function就可以表示成$L(\theta)$的形式，因为其大小完全取决于unknown parameters。

对于$\boldsymbol{\theta}=\begin{bmatrix}\theta_0 \\ \theta_1 \\ … \end{bmatrix}$，取loss function $L$对每个参数的偏函数在$\boldsymbol{\theta}_0$处的值，组成在点$\boldsymbol{\theta}^0$处的斜率$\boldsymbol{g}$：

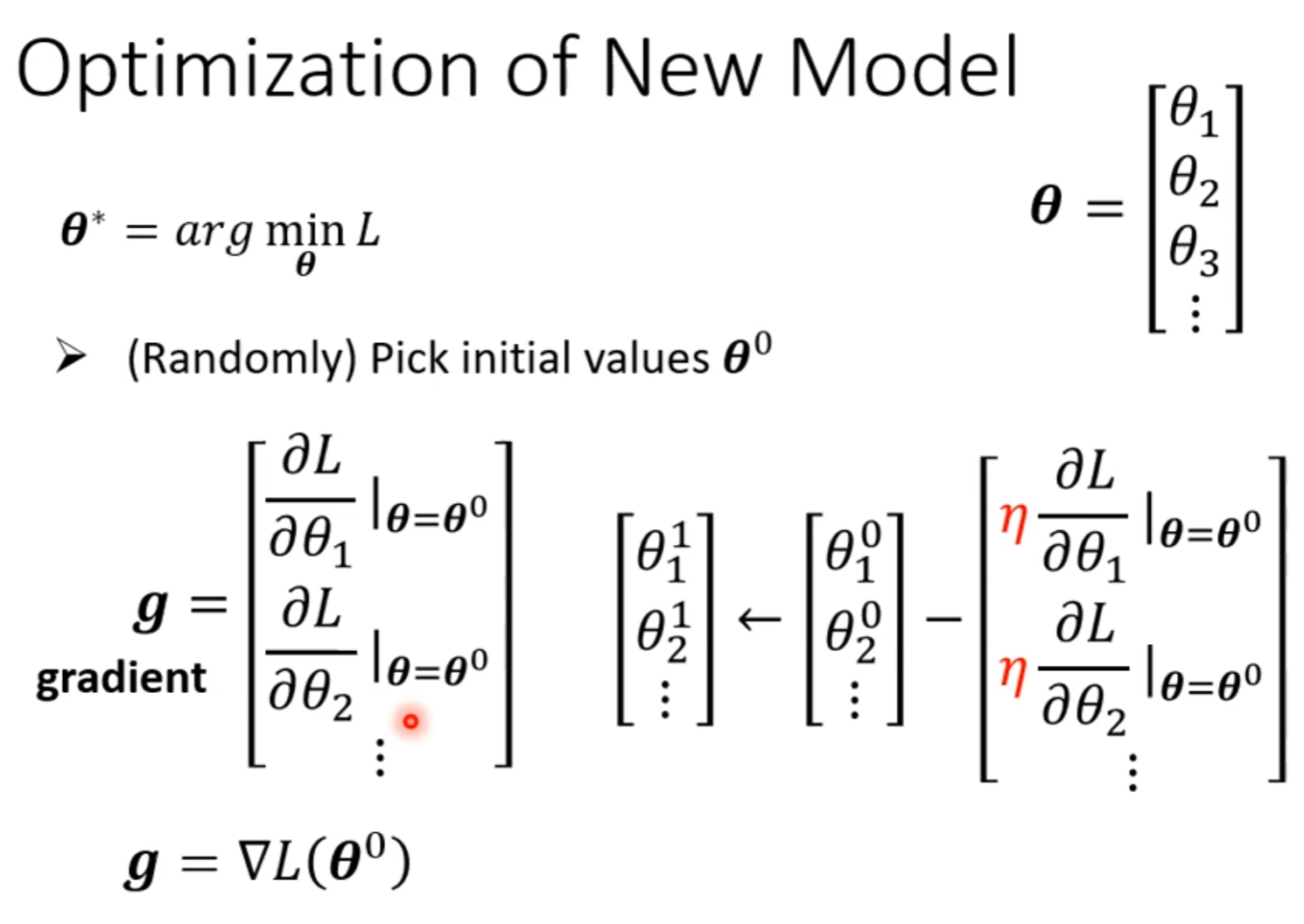
其中的$\eta$则为步长。
在实际的应用中，我们通常不会拿所有的数据来计算损失函数的值，而是将所有的数据数据进行任意随机等大小的分组（即batch）。进行梯度下降时，先算batch1的loss function，更新一次权重之后，再拿batch2的数据算一次loss function，更新权重，直到遍历完所有batch完成一次epoch。也就是有update的次数等于batch个数乘上epoch轮数
除了sigmoid之外，ReLU(Rectified Linear Unit)也是常用的激活函数。使用其表示时，有变式：$y = b + \sum_ic_isigmoid(b_i+\sum_jw_{ij}x_j)$变为了$y = b + \sum_{2i}c_imax(0, b_i+\sum_jw_{ij}x_j)$。其中ReLU使用2倍的i是因为ReLU需要两个才能拼出一个hard sigmoid形状
除了改变激活函数之外，还可以增加层数：

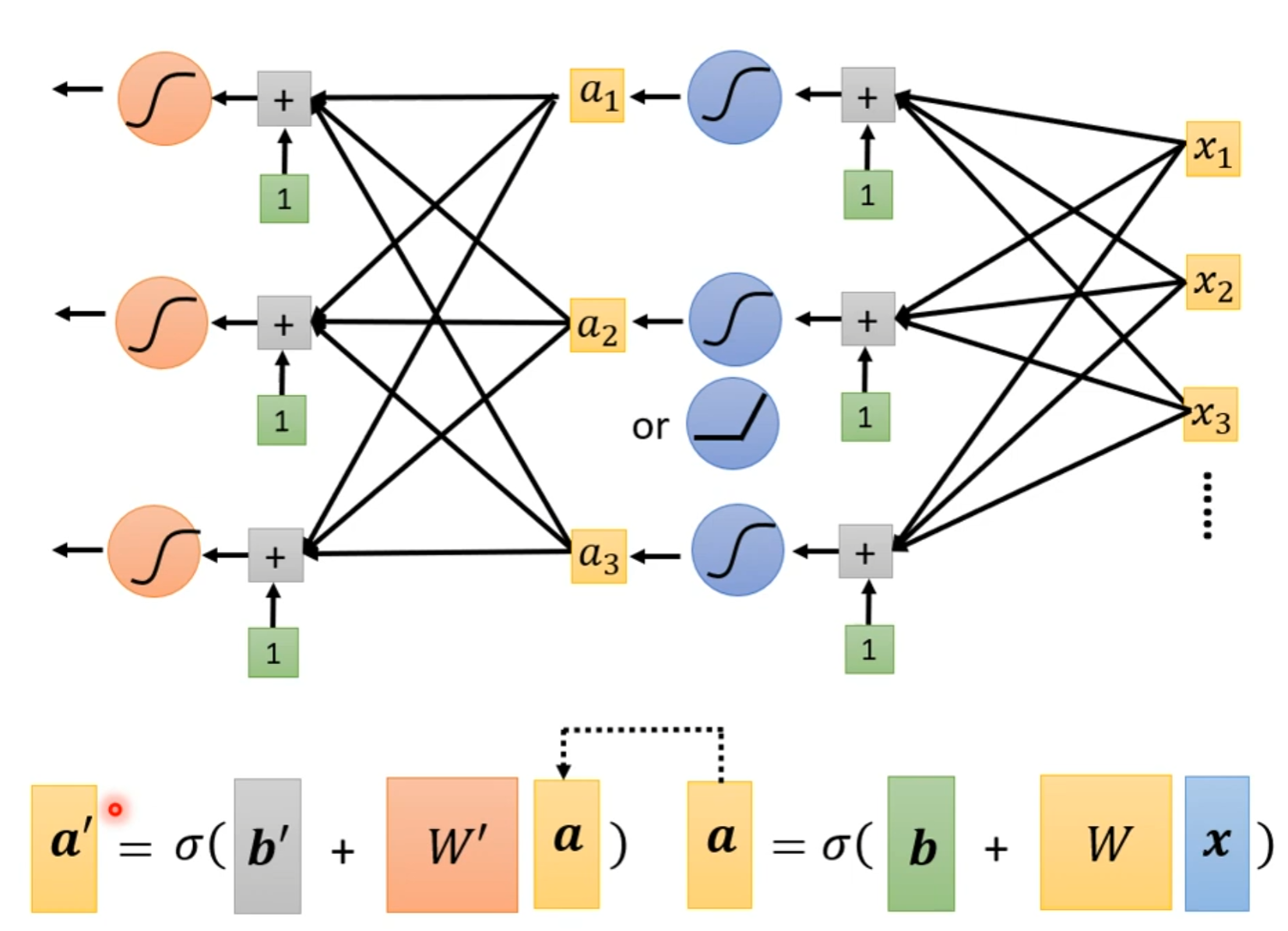
也就是将前一层的激活函数的输出再作为新的特征输入给下一层进行迭代。

经验上而言，层数的递增的确能提高正确率，有：
1. AlexNet(2012)：8层，16.4%错误率
2. VGG(2014)：19层，7.3%错误率
3. GoogleNet(2014)，22层，6.7%错误率
4. Residual Net(2015)，152层，3.56%错误率。其训练深度网络时还通过特殊的网络结构来进行了优化。
过于复杂的结构（如选取过多特征、或者网络层数越大）可能导致在训练集上效果更好，但测试集上反而效果变差的情况，这种情况便称为overfitting过拟合

Roadmap of Improving Model

总体roadmap如下图所示：
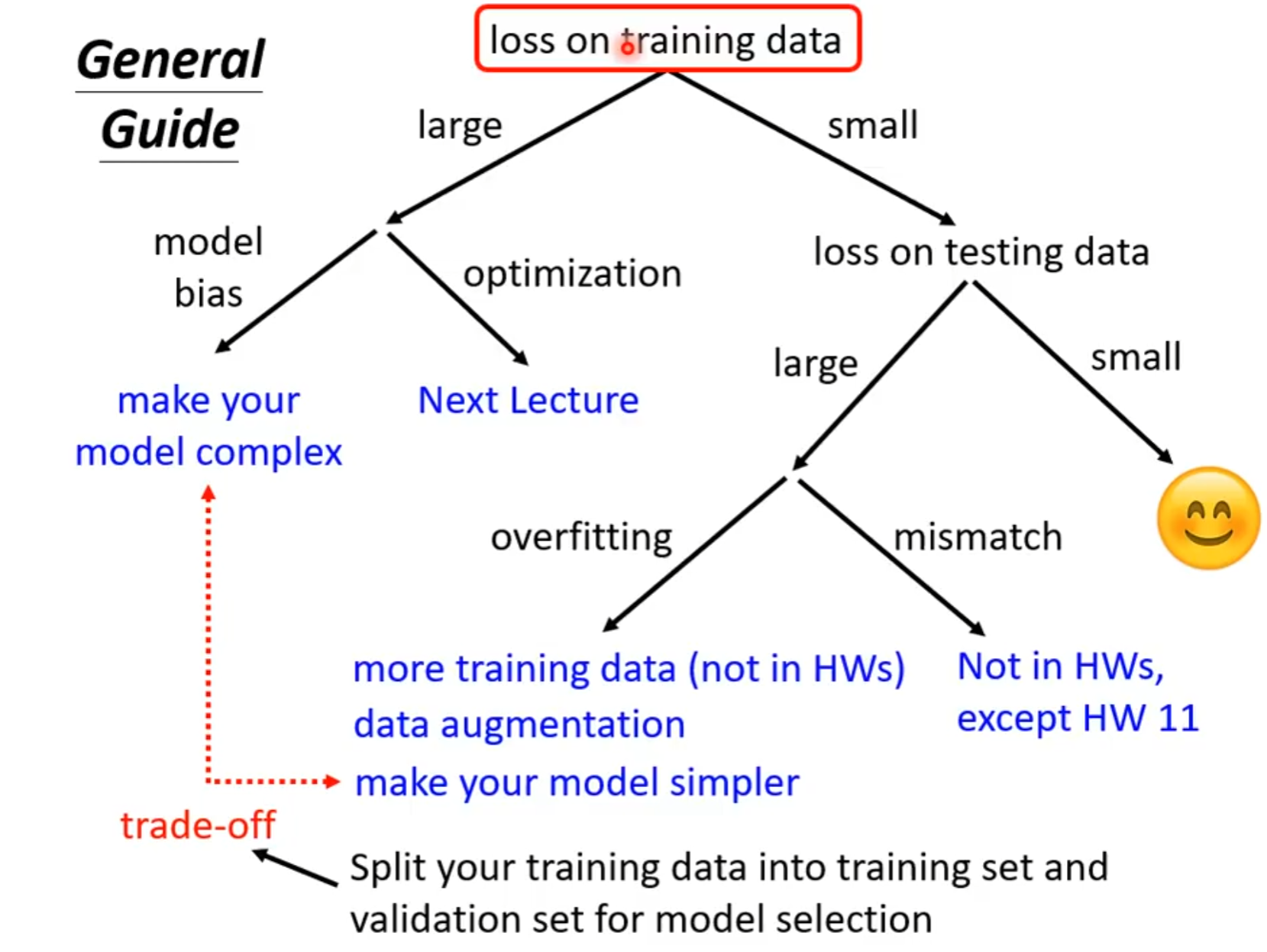
如何判断在训练集上loss过大的原因到底是model能力不足（无法得到很好的结果），还是梯度下降没有得到更好的点（可能有更好的结果，但却没有去找到它）呢？课程中给出的方法分为如下几步：
1. 首先从更简单的模型开始训练起，如使用更少的层数、更少的特征、甚至是非深度学习的其他机器学习方法等等
2. 而如果与之相对的，当我们基于上一步的方法做更多层数的模型训练时，如果我们不能得到更好的training loss时，我们则认为是优化方面的问题（因为更多层数的模型一定能包含浅层数模型的能力）
但也不是说对于一个模型，更大的深度就一定更好，更大的深度代表模型的弹性越大，在同样的训练集上训练出来的函数在非训练集上的表现就可能越复杂，从而有更大可能产生过拟合的现象，即模型在training data上表现良好，但在测试集上表现一般甚至很差的现象。如何解决过拟合的问题
1. 增加训练资料
  1. 最好是直接增加实际的训练资料
  2. Data augmentation：在原有的训练集上，根据自己的理解，创造新的训练资料（比如对于图像识别，将原来的图像放大缩小、反转、切取部分等等，但一般不会把图片上下颠倒，因为日常图像识别中也不会出现上下颠倒的照片，这样处理反而可能会造成学习不希望学习的东西）
2. 缩小模型的弹性：
  1. Less paremeters、sharing parameters，如fully-connect网络中的CNN，就是针对图像识别做了一些限制，使得其弹性没有普通全连接网络的弹性那么高，但是在图像识别上表现更好
  2. Less features
  3. Early stopping
  4. Regulation
  5. Dropout
从上述流程中也可以看到，overfitting和model bias之间实际存在着一个trade-off的问题

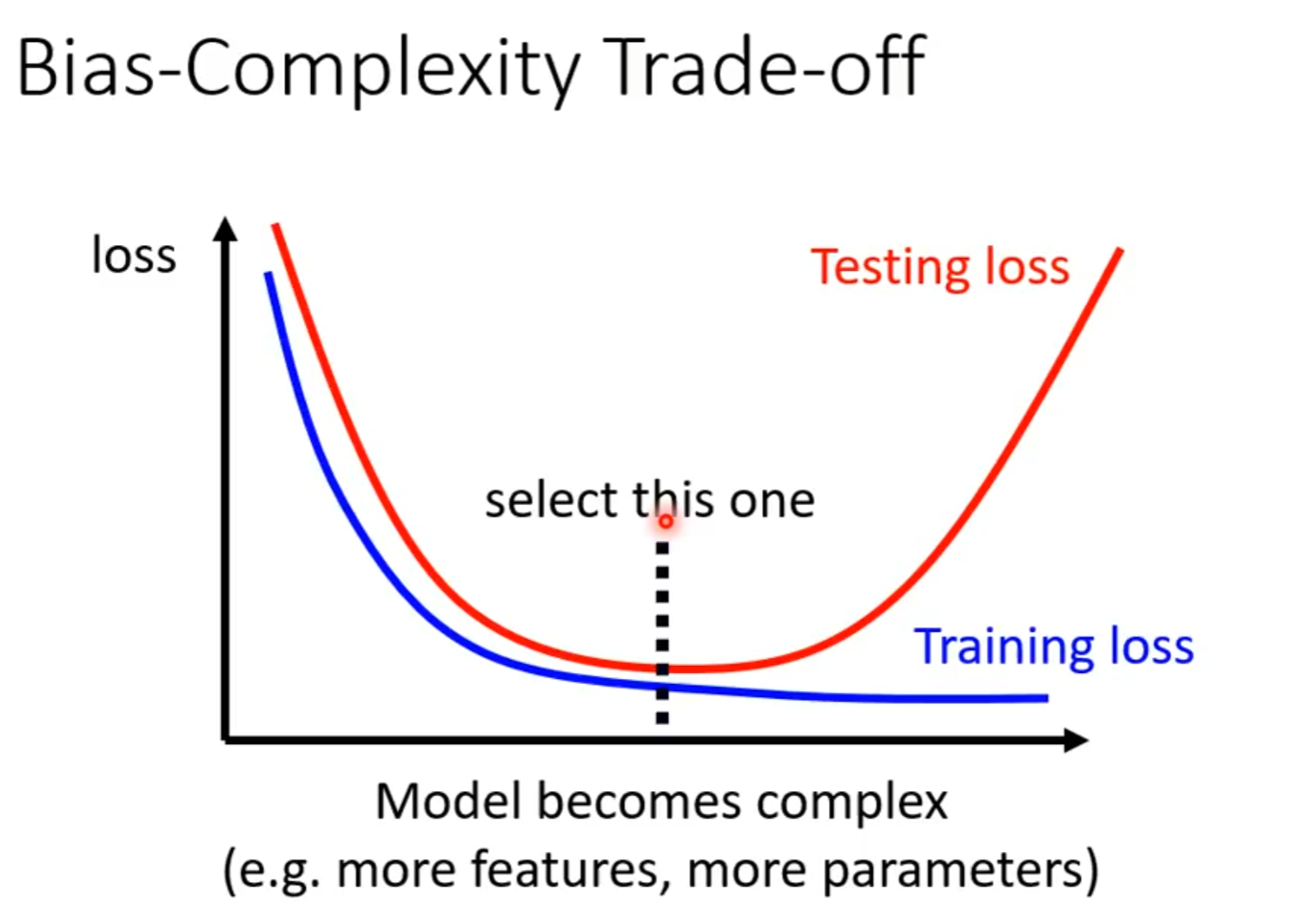
一种朴素的想法是，在测试集的公开部分(public testing set)上对多个训练的模型进行比较，选择其中mse最小的模型，再拿去在测试集的真正拿来测试的部分(private testing set)上验证，往往导致如下的情况出现：

因此，真正好的训练流程是，在原来的训练集(training set)上将数据分为training set和validation set 两部分，从而让原来的public testing set有了private testing set的效果，这样训练出来的模型就能在private testing set上表现更好。

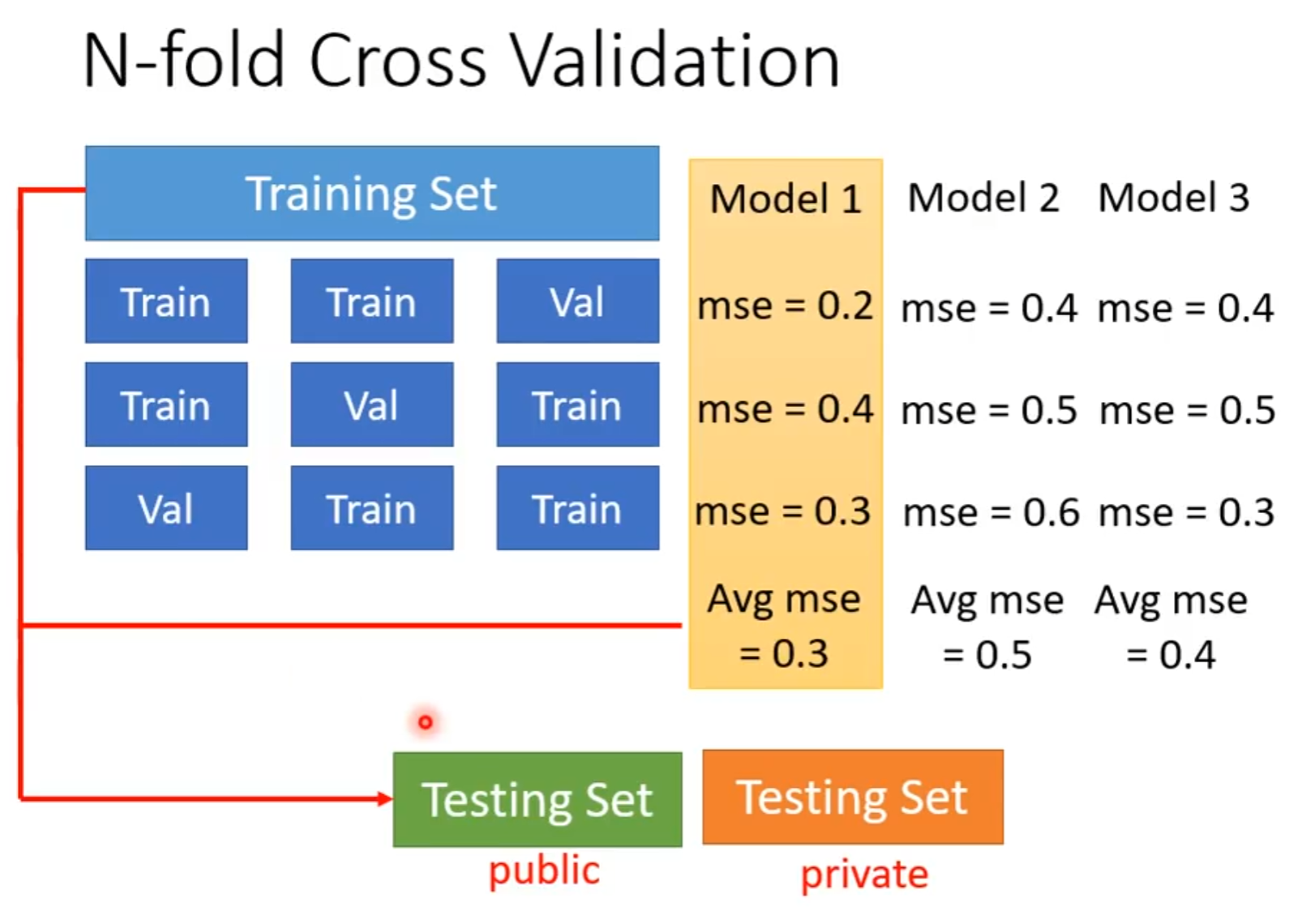
而关于如何将training set进行train和val的切分，N-fold Cross Validation的方法被提出，其将数据集等分为若干份（如等分为3份）然后交叉来作为训练集和验证集，每个模型都对每一种交叉后的数据集进行训练和验证，得到在每种验证集上的mse后取平均，来得到最终表现最好的模型。如图所示：

当然，除了上述的overfitting，导致在测试集上表现不佳的原因还有就是实际数据和测试数据的分布不同的问题（mismatch），这种就很难通过改进模型来解决

PREVIOUSrust学习

NEXT机器学习&深度学习